The Problem Normalization Addresses: Internal Covariate Shift
Before diving into the specifics, it’s crucial to understand the problem these techniques aim to solve: Internal Covariate Shift.
- Covariate Shift: In machine learning, covariate shift refers to the change in the distribution of the input to a model between training and testing.
- Internal Covariate Shift (ICS): In deep neural networks, ICS refers to the change in the distribution of network activations within the network during training. As the parameters of earlier layers change, the input distribution to later layers also changes.
Why is ICS a problem?
- Training Instability: ICS can make training slower and more difficult. Each layer needs to constantly adapt to the changing input distribution, making it harder for the network to learn stable representations.
- Vanishing/Exploding Gradients: ICS can contribute to the vanishing and exploding gradient problems, especially in deep networks.
- Slower Convergence: The constant adaptation to shifting distributions slows down the convergence of the training process.
Normalization Techniques: The Solutions
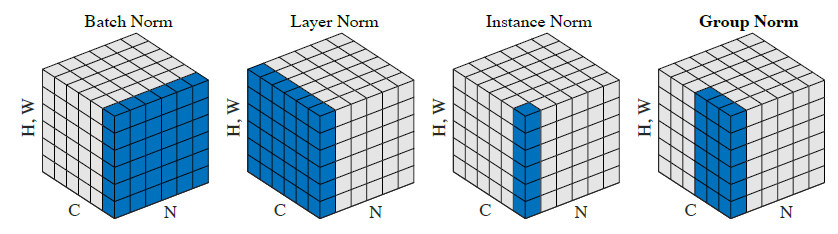
| Feature | Batch Normalization (BatchNorm) | Layer Normalization (LayerNorm) | Group Normalization (GroupNorm) |
|---|---|---|---|
| Normalization Dimension | Batch (N) per channel (C) | Feature (C, H, W) per sample (N) | Batch (N) within channel groups |
| Batch Size Dependence | Highly dependent, degrades with small batches | Independent, works well with small batches | Less dependent than BatchNorm, works well with small batches |
| Suitable Architectures | CNNs (with large batches) | RNNs, Transformers, CNNs | CNNs (especially with small batches), Object Detection, Segmentation |
| Synchronization across GPUs | Required for batch statistics | Not required | Not required |
| Inference Behavior | Uses moving averages of batch statistics | Consistent with training | Consistent with training |
| Hyperparameters | None (besides learnable scale/shift) | None (besides learnable scale/shift) | Number of groups (G), learnable scale/shift |
| Strengths | Effective with large batches, speeds up training, regularization effect | Batch size independent, works well with sequences, consistent inference | Good for small batches, balances batch and feature normalization, effective in object detection |
| Weaknesses | Batch size sensitive, not ideal for RNNs, synchronization needed, inference discrepancies | May be less effective than BatchNorm for CNNs in some cases, might lose feature relationships | Hyperparameter tuning for number of groups, may not outperform BatchNorm with large batches |