SDEs and ODEs

Differential equation

Equation that find solution as a function, the general form of a first-order ordinary differential equation (ODE) is:

$$dx(t)/dt=f(t,x(t))$$

The equation says:

“The rate of change of the quantity $x$ at time $t$ is equal to some function $f$ that depends on the current time $t$ and the current value of $x$.”

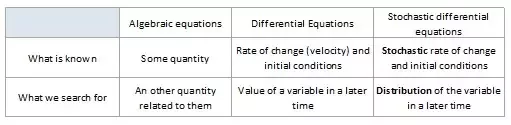
Stochastic Differential Equations (SDEs)

Stochastic Process describe system that evolve over time which inherently have some randomness (e.g. stock market, climate model) and we can use SDEs to model Stochastic Process. Summary from great explanation about what SDEs is:

1. ODEs vs. SDEs - The Core Difference: Noise

   1. ODEs: Model deterministic systems. Given an initial condition, the future behavior of the system is completely determined. The equation $dx(t)/dt=f(t,x(t))$ describes a system where the rate of change is solely a function of the current state and time.
   2. SDEs: Model systems with randomness or “noise.” The future behavior is not entirely predictable, even with the same initial condition, because random disturbances influence the system’s evolution.

2. Modeling Noise

   1. Normally Distributed Noise (Wiener Process/Brownian Motion): Represents continuous, small fluctuations. Think of it as the cumulative effect of many tiny, independent random influences. It is suitable for situations where the randomness is relatively well-behaved.
   2. Lévy Noise (Jump Noise): Represents sudden, discontinuous jumps. Good for modeling abrupt changes or rare, high-impact events (like the dog suddenly interfering with the ball or a sudden crash in the stock market).

3. The SDE Equation: We add noise term to ODE:

   $$dx(t)/dt=f(t,x(t))+noise$$

   and people define noise as:

   $$d{X}_t=f(t,X_t)dt+\sigma (t,X_t)d{W}_t$$
   • $X_t$: The state of the system at time $t$ (analogous to $x(t)$ in the ODE). This is now a random variable because its value is influenced by the noise.
   • $f(t,X_t)dt$: The deterministic part, similar to the ODE. It describes the “drift” or the average tendency of the system’s evolution.
   • $\sigma (t,X_t)d{W}_t$: The stochastic part, representing the influence of the noise.
     • $d{W}_t$: The increment of the Wiener process (Brownian motion) at time $t$. It’s a random variable, typically normally distributed with mean 0 and variance $dt$.
     • $\sigma (t,X_t)$: The diffusion coefficient. It scales the noise and can depend on both time and the current state of the system. It determines the intensity of the random fluctuations.

4. Solutions to SDEs

   1. ODEs: We typically seek a unique, deterministic solution $x(t)$ that satisfies the equation and an initial condition.
   2. SDEs: Due to the randomness, we can’t find a single, exact solution in the same way. Instead, we consider:
      • Sample-Path Solutions: These describe the evolution of the system for a specific realization of the noise. If you simulate the SDE many times, each simulation will generate a different sample path because the noise will be different each time. These solutions still depend on initial conditions.
      • Distributional Solutions: Instead of focusing on individual paths, we look at the probability distribution of $X_t$ at different times. This tells us the likelihood of the system being in different states at a given time. For example, the text mentions that the ball, after rolling down the noisy hill for a while, might be distributed around the bottom of the hill according to a normal distribution.